0%

(CVPR 2019) MnasNet:Platform-Aware Neural Architecture Search for Mobile

Posted on In , ,

Keyword [Policy Gradient] [NAS] [Mobile Device] [MNASNet]

Tan M, Chen B, Pang R, et al. Mnasnet: Platform-aware neural architecture search for mobile[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019: 2820-2828.


1. Overview

1.1. Motivation

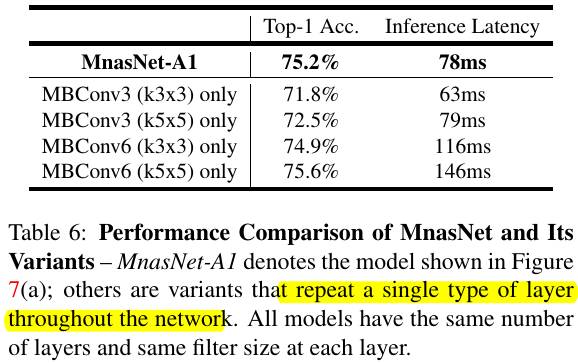
1) Existing methods mainly search for a few types of cells and then repeatedly stack.
2) Existing methods process on small tasks, CIFAR.

In this paper, it proposes MNASNet (Automated Mobile Neural Architecture Search)

1) Incorporate model latency into the main objective.
2) Measure latency by executing on mobile phone.
3) Novel search space. For each block, search layer then stack.




1.2. Contribution

1) Multi-objective neural architecture search.
2) Factorized hierarchical search space.

2. Related Work

1) Quantization.
2) Pruning.
3) Hand-craft.
4) NAS. RL, evolutionary search, differentiable search

3. Formulation



Pareto Optimal Solutions.
1) Has the highest ACC without increasing LAT.
2) Has the lowest LAT without decreasing ACC.




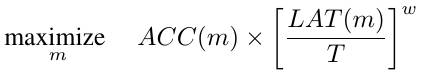
To ensure Pareto-optimal solutions have similar reward under different accuracy-latency trade-offs. set $\alpha=\beta=-0.07$

4. MNAS

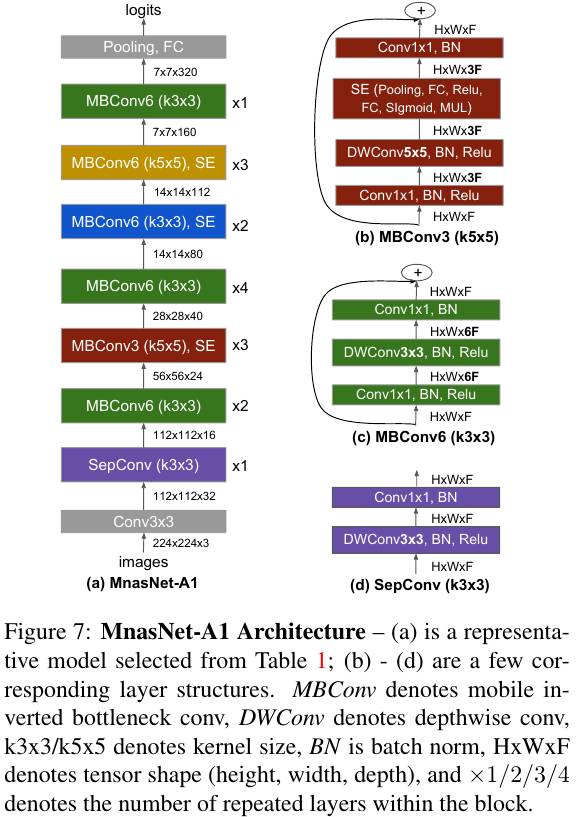
4.1. Factorized Hierarchical Search Space



1) Partition a CNN model into a sequence of pre-defined blocks.
2) Each block has a list of identical layers, whose operation and connections are determined by a per-block sub search space.
3) Choices

  • ConvOP: Conv, DWConv, Mobile Inverted Bottleneck Conv.
  • Kernel Size: $3\times 3$, $5 \times 5$.
  • SkipOp: Pooling, Indentity Residual, no skip.
  • Filter Num: $F_i$. {0.75, 1.0, 1.25} based on MobileNetV2.
  • Layer Num: $N_i$. {0, 1, -1} based on MobileNetV2.

4.2. Search Algorithm



1) $m$. a sample model determined by action $a_{1:T}$.
2) $R$. reward value.
3) Controller sample a batch of models, by predicting a sequence of tokens.
4) Controller are updated by maximizing the expected reward using Proximal Policy Optimization (PPO).

5. MNASNet



1) Same RNN Controller as NASNet.
2) Each architecture search takes 4.5 days on 64 TPUv2 devices.
3) Set $T=75ms$.

6. Experiments